Diffusion Probabilistic Models for 3D Point Cloud Generation

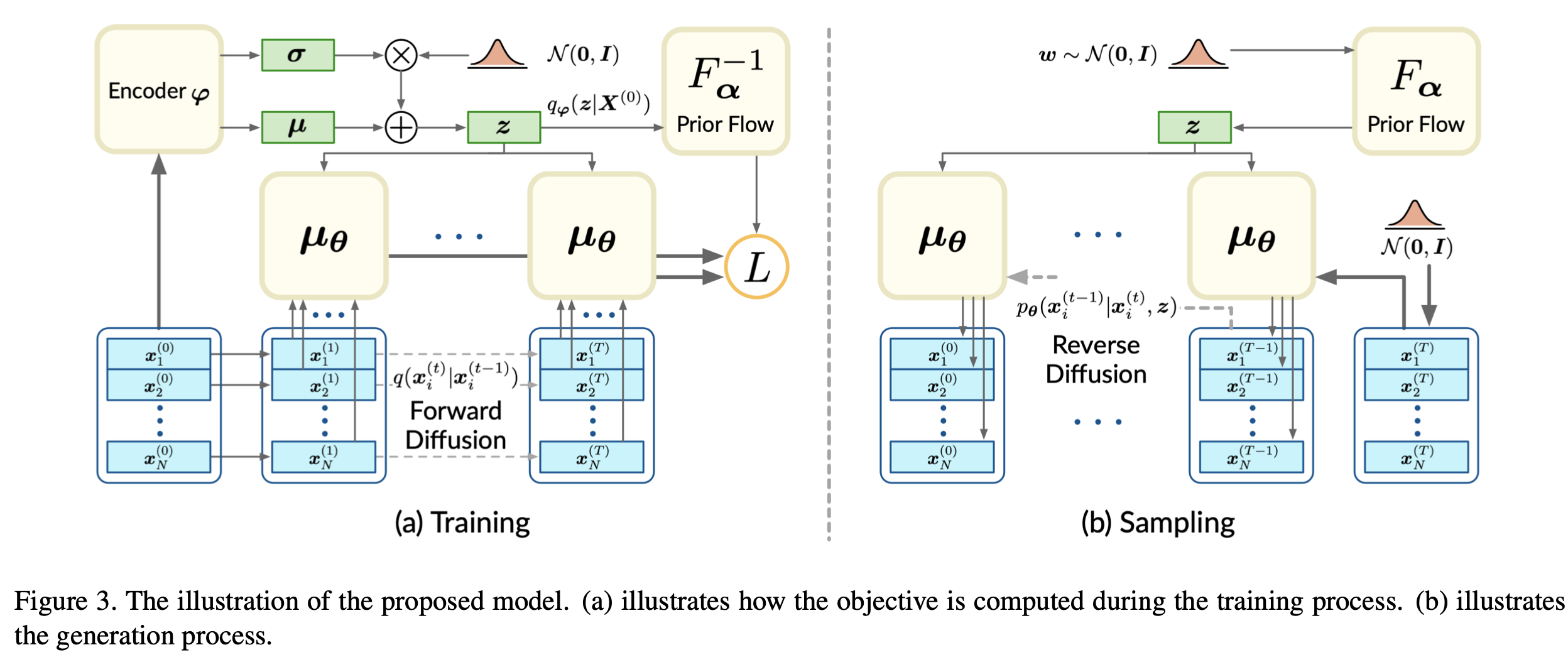
Overview

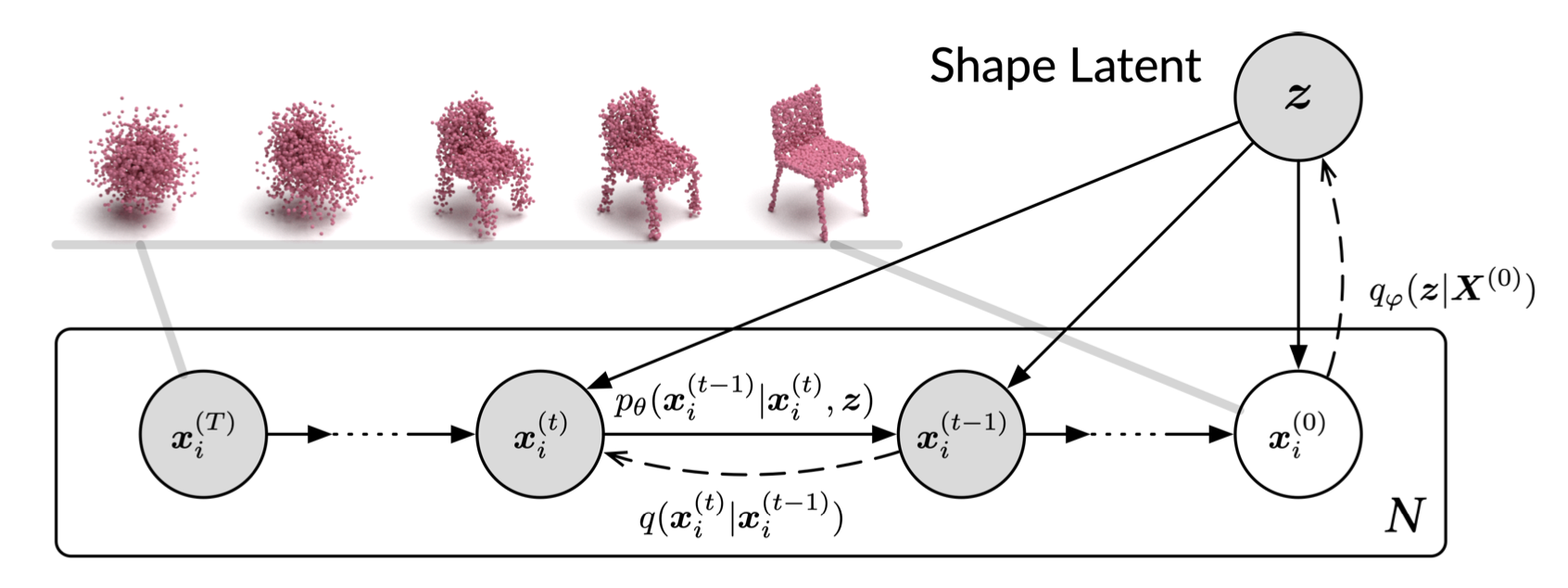
Define a point cloud $X^{(0)} = \{x_i^{(0)}\}_{i=1}^N$, where $N$ is the number of points and for each point $x_i$, we can denote as $q(x_i\vert z)$, where $z$ is the shape latent that determines the distribution of points.

The forward process can be modeled as: $\begin{align} q(x_i^{(1:T)}|x_i^{(0)}) &= \prod_{t=1}^T q(x_i^{(t)}|x_i^{(t-1)}) \\ q(x^{(t)}|x^{(t-1)}) &= \mathcal{N}(x^{(t)}|\sqrt{1-\beta_t}x^{(t-1)}, \beta_t I) \end{align}$

The reverse process is defined as: $\begin{align} p_\theta(x^{(0:T)}|z) &= p_\theta(x^{(T)})\prod_{t=1}^T p_\theta(x^{(t-1)}|x^{(t)}, z) \\ p_\theta(x^{(t-1)}|x^{(t)},z) &= \mathcal{N}(x^{(t-1)}; \mu_\theta(x^{(t)}, t, z), \beta_t I) \end{align}$

For the whole point cloud $X$ $\begin{align} q(X^{(1:T)}|X^{(0)}) &= \prod_{i=1}^N q(x_i^{(1:T)}|x_i^{(0)}) \\ p_\theta(X^{(0:T)}|z) &= \prod_{i=1}^N p_\theta(x_i^{(0:T)}|x_i^{(0)}) \end{align}$

Loss

Loss function see original paper.

Train